Compare Fits in Curve Fitter App

Interactive Curve Fitter Workflow

The next topics fit census data using polynomial equations up to the sixth degree, and a single-term exponential equation. The steps demonstrate how to:

Load data and explore various fits using different library models.
Search for the best fit by:
- Comparing graphical fit results
- Comparing numerical fit results including the fitted coefficients and goodness-of-fit statistics
Export your best fit results to the MATLAB^® workspace to analyze the model at the command line.
Save the session and generate MATLAB code for all fits and plots.

Loading Data and Creating Fits

You must load the data variables into the MATLAB workspace before you can fit data using the Curve Fitter app. For this example, the data is stored in the MATLAB file census.mat.

Load the data.
```
load census
```
The workspace contains two new variables.
- cdate is a column vector containing the years 1790 to 1990 in 10-year increments.
- pop is a column vector with the US population figures that correspond to the years in cdate.
Open the Curve Fitter app.
```
curveFitter
```
On the Curve Fitter tab, in the Data section, click Select Data. In the Select Fitting Data dialog box, select the variable names cdate and pop from the X data and Y data lists, respectively.
The Curve Fitter app creates and plots a default fit to the X input (or predictor) data and the Y output (or response) data. The default fit is a linear polynomial fit type. Observe the fit settings display in the Fit Options pane. The fit is a first-degree polynomial.
In the Fit Options pane, change the fit to a second-degree polynomial by selecting 2 from the Degree list.
The Curve Fitter app plots the new fit. The Curve Fitter app calculates a new fit when you change fit settings because Auto is selected by default. If refitting is time consuming, as is sometimes the case for large data sets, you can turn off the automatic behavior. On the Curve Fitter tab, in the Fit section, select Manual.
The Curve Fitter app displays results of fitting the census data with a quadratic polynomial in the Results pane, where you can view the library model, fitted coefficients, and goodness-of-fit statistics.
Change the name of the fit. In the Table Of Fits pane, double-click untitled fit 1 in the Fit name column and type poly2.
Display the residuals. On the Curve Fitter tab, in the Visualization section, click Residuals Plot.
The residuals indicate that a better fit might be possible. Therefore, continue exploring various fits to the census data set.
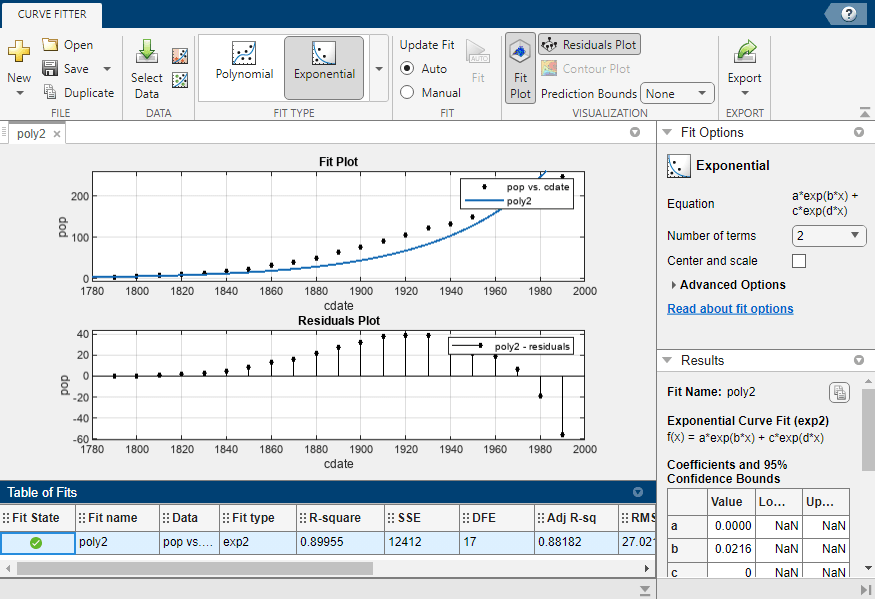
Add new fits to try the other library equations.
1. Right-click the fit in the Table Of Fits pane, and select Duplicate "poly2". Alternatively, on the Curve Fitter tab, in the File section, click Duplicate.
  Tip
  For fits of a given type (for example, polynomials), duplicate a fit instead of creating a new fit because copying a fit requires fewer steps. The duplicated fit contains the same data selections and fit settings.
2. Change the polynomial Degree to 3 and rename the fit poly3.
3. When you fit higher degree polynomials, the Results pane displays this warning.
  Equation is badly conditioned. Remove repeated data points or try centering and scaling.
  Normalize the data by selecting the Center and scale check box in the Fit Options pane.
4. Repeat steps a and b to add polynomial fits up to the sixth degree. Then add an exponential fit. On the Curve Fitter tab, in the File section, click New and select New Fit. In the Fit Type section, click the arrow to open the gallery, and click Exponential in the Regression Models section.
5. For each new fit, look at the Results pane information, and the residuals plot in the app.
  The residuals from a good fit should look random with no apparent pattern. A pattern, such as a tendency for consecutive residuals to have the same sign, can be an indication that a better model exists.

About Scaling

The warning about scaling arises because the fitting procedure uses the cdate values as the basis for a matrix with very large values. The spread of the cdate values results in a scaling problem. To address this problem, you can normalize the cdate data. Normalization scales the predictor data to improve the accuracy of the subsequent numeric computations. For example, you can normalize cdate by centering and scaling the data to have zero mean and unit standard deviation.

(cdate - mean(cdate))./std(cdate)

Note

Because the predictor data changes after normalizing, the values of the fitted coefficients also change when compared to the original data. However, the functional form of the data and the resulting goodness-of-fit statistics do not change. Additionally, the data is displayed in the Curve Fitter app plots using the original scale.

Determining the Best Fit

To determine the best fit, you should examine both the graphical and numerical fit results.

Examine the Graphical Fit Results

Determine the best fit by examining the graphs of the fits and residuals. To view plots for each fit in turn, click the fit in the Table Of Fits pane. The graphical fit results indicate that:
- The fits and residuals for the polynomial equations are all similar, making it difficult to choose the best one.
- The fit and residuals for the single-term exponential equation indicate it is a poor fit overall. Therefore, it is a poor choice and you can remove the exponential fit from the candidates for best fit.
Examine the behavior of the fits after the year 2000. The goal of fitting the census data is to extrapolate the best fit to predict future population values.
1. Click the sixth-degree polynomial fit in the Table Of Fits pane to view the plots for this fit.
2. In the fit plot, click the Pan button in the axes toolbar and pan until the fit is visible for several years after the year 2000. The axes limits of the residuals plot adjust accordingly.
3. Examine the fit plot. The behavior of the sixth-degree polynomial fit beyond the data range makes it a poor choice for extrapolation and you can reject this fit.

Evaluate the Numerical Fit Results

When you can no longer eliminate fits by examining them graphically, you should examine the numerical fit results. The Curve Fitter app displays two types of numerical fit results:

Goodness-of-fit statistics
Confidence bounds on the fitted coefficients

The goodness-of-fit statistics help you determine how well the curve fits the data. The confidence bounds on the coefficients determine their accuracy.

Examine the numerical fit results.

For each fit, view the goodness-of-fit statistics in the Results pane.
Compare all fits simultaneously in the Table Of Fits pane. Click the column headings to sort by statistics results.
Examine the sum of squares due to error (SSE) and the adjusted R-square statistics to help determine the best fit. The SSE statistic is the least-squares error of the fit, with a value closer to zero indicating a better fit. The adjusted R-square statistic is generally the best indicator of the fit quality when you add additional coefficients to your model.
The largest SSE for exp indicates it is a poor fit, which you already determined by examining the fit and residuals. The lowest SSE value is associated with poly6. However, the behavior of this fit beyond the data range makes it a poor choice for extrapolation, so you already rejected this fit by examining the plots with new axes limits.
The next best SSE value is associated with the fifth-degree polynomial fit, poly5, suggesting it might be the best fit. However, the SSE and adjusted R-square values for the remaining polynomial fits are all very close to each other.
Resolve the best fit issue by examining the confidence bounds for the remaining fits in the Results pane. Click a fit in the Table Of Fits pane to open the fit figure (or select it, if the figure is already open), and view the Results pane. Each fit figure displays the plots for a single fit.
Display the fifth-degree polynomial poly5 and the second-degree polynomial poly2 fit figures side by side. Examining results side by side can help you assess fits.
1. To show two fit figures simultaneously, you can drag and drop the fit figure tabs in the Fits pane. Alternatively, you can click the Document Actions button located to the far right of the fit figure tabs. Select the Tile All option and specify a 1-by-2 or 2-by-1 layout.
2. Compare the coefficients and bounds (p1, p2, and so on) in the Results pane for both fits, poly5 and poly2. The toolbox calculates 95% confidence bounds on coefficients. The confidence bounds on the coefficients determine their accuracy. Check the equations in the Results pane (f(x)=p1*x+p2*x...) to see the model terms for each coefficient. Note that p2 refers to the p2*x term in Poly2 and the p2*x^4 term in Poly5. Do not compare normalized coefficients directly with non-normalized coefficients.
  Tip
  If you want more space to view and compare plots and results, as shown next, drag down the Table Of Fits pane. You can also hide the Results pane to show only plots.
  The bounds cross zero on the p1, p2, and p3 coefficients for the fifth-degree polynomial. This means you cannot be sure that these coefficients differ from zero. If the higher order model terms might have coefficients of zero, they are not helping with the fit, which suggests that this model overfits the census data.
  However, the small confidence bounds do not cross zero on p1, p2, and p3 for the quadratic fit poly2, indicating that the fitted coefficients are known fairly accurately.
  Therefore, after examining both the graphical and numerical fit results, you should select poly2 as the best fit to extrapolate the census data.

Note

The fitted coefficients associated with the constant, linear, and quadratic terms are nearly identical for each normalized polynomial equation. However, as the polynomial degree increases, the coefficient bounds associated with the higher degree terms cross zero, which suggests overfitting.

Analyzing Best Fit in the Workspace

You can export the selected fit and the associated fit results to the MATLAB workspace. On the Curve Fitter tab, in the Export section, click Export and select Export to Workspace. The fit is saved as a MATLAB object and the associated fit results are saved as structures.

Right-click the poly2 fit in the Table Of Fits pane, and select Save "poly2" to Workspace. Alternatively, click Export and select Export to Workspace. The app opens a dialog box.

Click OK to save the fit with the default names.

fittedmodel is saved as a Curve Fitting Toolbox™ cfit object.

whos fittedmodel

  Name             Size            Bytes  Class    Attributes

  fittedmodel      1x1               925  cfit

Examine the cfit object fittedmodel to display the model, the fitted coefficients, and the confidence bounds for the fitted coefficients.

fittedmodel

     Linear model Poly2:
     fittedmodel(x) = p1*x^2 + p2*x + p3
     Coefficients (with 95% confidence bounds):
       p1 =    0.006541  (0.006124, 0.006958)
       p2 =      -23.51  (-25.09, -21.93)
       p3 =   2.113e+04  (1.964e+04, 2.262e+04)

Examine the goodness structure to display goodness-of-fit results.

goodness

goodness = 

  struct with fields:

           sse: 159.0293
       rsquare: 0.9987
           dfe: 18
    adjrsquare: 0.9986
          rmse: 2.9724

Examine the output structure to display additional information associated with the fit, such as the residuals.

output

output = 

  struct with fields:

        numobs: 21
      numparam: 3
     residuals: [21×1 double]
      Jacobian: [21×3 double]
      exitflag: 1
     algorithm: 'QR factorization and solve'
    iterations: 1

You can evaluate (interpolate or extrapolate), differentiate, or integrate a fit over a specified data range with various postprocessing functions.

For example, evaluate fittedmodel at a vector of values to extrapolate to the year 2050.

x = 2000:10:2050;
y = fittedmodel(x)

Plot the fit to the census data and the extrapolated fit values.

plot(fittedmodel,cdate,pop)
hold on
plot(fittedmodel,x,y,"k+")
hold off
legend(["data","","extrapolated data","fitted curve"], ...
  "Location","northwest")

Fit plot using census data and extrapolated values

For more examples and instructions for interactive and command-line fit analysis, and a list of all postprocessing functions, see Fit Postprocessing.

For an example reproducing this interactive census data analysis using the command line, see Polynomial Curve Fitting.

Saving Your Work

The Curve Fitter app provides several options for saving your work. You can save one or more fits and the associated fit results as variables to the MATLAB workspace. You can then use this saved information for documentation purposes, or to extend your data exploration and analysis. In addition to saving your work to MATLAB workspace variables, you can:

Save the current curve fitting session. On the Curve Fitter tab, in the File section, click Save and select Save Session. The session file contains all the fits and variables in your session and remembers your layout. See Save and Reopen Sessions.
Generate MATLAB code to recreate a fit and its associated plots. In the Export section, click Export and select Generate Code. The Curve Fitter app generates code for the currently selected fit and displays the file in the MATLAB Editor.
You can recreate your fit and plots by calling the file at the command line with your original data as input arguments. You can also call the file with new data, and automate the process of fitting multiple data sets. For more information, see Generating Code from the Curve Fitter App.